Les hypothèses sont :
- La densité moyenne des étoiles donc la luminosité moyenne qu'elles engendrent dans une unité de volume ne varie pas dans l'espace.
- Cette luminosité moyenne ne varie pas avec le temps.
- Les étoiles ne sont pas animées de grands mouvements systématiques.
- L' espace est euclidien.
- Les lois de la physique s'appliquent à l'ensemble de la physique observable.
Construisons des sphères imaginaires centrées sur nous avec des étoiles uniformément distribuées dans l’espace.
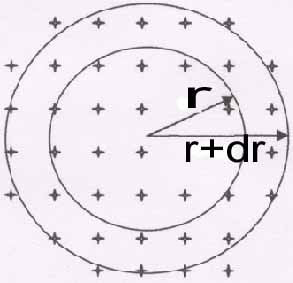
n : nombre d’étoiles
ρ : densité volumique d’étoiles
dn = 4π r2dr.ρ : nombre d’étoiles dans une couche d’épaisseur dr avec un rayon r
or I(r)
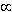 1/r2 : intensité lumineuse reçue d’une étoile distant de r
1/r2 : intensité lumineuse reçue d’une étoile distant de r
alors I(r).dn
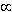 4πρ.dr = constante :
on reçoit la même quantité de lumière de chaque couche.
4πρ.dr = constante :
on reçoit la même quantité de lumière de chaque couche.
Or
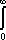 I(r).dn
=
I(r).dn
=
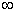 , donc si l’univers est infini nous devrions recevoir une quantité infinie de lumière
stellaire.
, donc si l’univers est infini nous devrions recevoir une quantité infinie de lumière
stellaire.
Jean-Philippe Loys de Chéseaux
En 1743 dans son « Traité de la comète », Chéseaux reprend la démonstration précédente en y ajoutant le fait que certaines étoiles lointaines sont cachées par des étoiles rapprochées. Donc la lumière totale augmente avec le nombre de couche sphérique mais lorsque le ciel est totalement recouvert d’étoiles, l’addition de couches supplémentaires n’accroît pas la lumière reçue.
Calcul de Chéseaux (exprimés en notation moderne et tels que Kelvin les a formulés en 1901)
Hypothèses :
- Toutes les étoiles sont semblables au soleil (même rayon :a)
- Espace uniformément répartit d’étoiles
Soit ρ :densité d’étoiles dans l’espace
Nombre d’étoiles dans une couche sphérique de rayon et d’épaisseur dr : N = 4 πρr2drSection géométrique d’une étoile (ou aire d’une étoile dans la couche sphérique) : σ = π a2
Donc la surface occupée par ces étoiles dans cette couche est : Se = N σ = 4 π2a2ρ r2dr
Or l’aire de cette coucheest : Sc=4πr2
Alors la fraction du ciel recouverte par les étoiles dans cette couche est :
D’où la fraction du ciel recouverte par les étoiles est :
α = 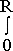 ρσdr = ρσR
ρσdr = ρσR
Donc si la sphère de rayon R est entièrement recouverte d’étoiles, on obtient la limite de visibilité (:λ) tel que :ρ σλ=1 d'où λ=1/(ρσ) (2)
Remarque
Puisque ρ est le nombre d’étoiles par unité de volume,σ est la section d’une étoile,
alors λ=1/(ρσ)est la distance moyenne entre deux étoiles.
λ≡libre parcours moyen d’un rayon lumineux.
(le libre parcours moyen est la distance moyenne
parcourue en ligne droite par une particule entre deux collisions consécutifs)
Or
V=1/ρ
(3)
: volume moyen occupé par une étoile
Donc
λ=V/σ
(4)
Limite de visibilité =
(Volume moyen occupé par une étoile)/(Section d’une étoile)
Le nombre d’étoiles nécessaire pour recouvrir le ciel est : N=4/3
πλ3ρ
D’après (3) & (4),
N=4/3πV2/σ3
Et donc, même dans un univers infini contenant une infinité d’étoiles, nous ne voyons qu’à une distance finie et qu’un nombre fini d’étoiles.
En appliquant la méthode photométrique de
James Gregory
( :Il faut comparer les étoiles les plus brillantes aux planètes
supérieurs en tenant compte de leurs tailles , de leur distances au soleil, et
la réflexion partielle de la lumière sur leur surface), Chéseaux estime que les
étoiles les plus brillantes étaient à 240 000
U.A.
(= 4
années lumière
).
Puis, il considère que
λ= 76.1010 U.A. (= 3.1015 années lumière).
Pour l’époque (et même maintenant), cette limite de visibilité était très grande ; il estime alors qu’un fluide capable d’absorbé la lumière dans l’espace, même très faiblement, pouvait résoudre le problème de la nuit noire.
Calcul de l’effet de l’absorption sur le problème de la nuit noire
D’après (1), la fraction du ciel recouverte par les étoiles dans une couche sphérique de
rayon r et d’épaisseur dr est :
ρσdr
Pour tenir compte de l’occultation due aux étoiles contenues dans les couches
intermédiaires, on multiplie
ρσdr
par
exp(-r/λ).
(La probabilité qu’un photon n’entre pas en collision,
mais arrive sans accident pour être observé à une distance de r est la même
supposition que le photon rencontre au hasard un obstacle. Les collisions se
passent indépendamment et à l’allure constante
λ-1
par unité de distance. La probabilité P(r) qui est la distance pour la première
collision est r est alors donnée par une distribution exponentielle :
P(r)=λ-1exp(-r/λ)
)
(Ainsi si r>λ, P(r) est très faible)
De plus pour inclure l’effet de l’absorption interstellaire, il faut le multiplier par exp(-r/μ) , où μ est le libre parcours moyen d’absorption. Ainsi, la fraction du ciel recouverte par les étoiles de cette couche est : λ -1exp(-(λ-1+α-1)r)dr
D’où
α = 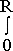 λ-1.exp[-(λ-1 + μ-1).r].dr
λ-1.exp[-(λ-1 + μ-1).r].dr
avec α : fraction du ciel recouverte par les étoiles non éclipsées
α = α(α+λ).[1-exp(-(λ-1+α).R)]
Lorsque r tend vers l'infini dans un Univers uniforme et illimité, cette fraction devient
:
Si l'absorption interstellaire est négligeable et si la limite d'absorption μ est très supérieure à la limite de visibilité λ, α est alors égal à l'unité et le ciel est entièrement recouvert d'étoiles non éclipsées. Mais, si l'absorption interstellaire est importante et si la limite d'absorption est très petite devant la limite de visibilité λ, alors α=μ/λ , et la majorité des étoiles reste masquée aux regards. Ainsi qu'il est dit dans le texte, la condition pour que l'obscurité résulte de l'existence d'un milieu absorbant est que la limite d'absorptionμ soit très inférieure à la limite de visibilitéλ.
Heinrich Wilhelm OlbersEn 1823, Olbers publia un article intitulé « Sur la transparence du ciel » (Voir Annexe ). Olbers fit le même type de calcul que Chéseaux sans cité les travaux de celui-ci; et l’énigme de l’obscurité fut plus tard baptisé : « paradoxe d’Olbers » et non de Chéseaux.
C’est à Olbers que l’on doit l’argument de la ligne de visée :
« Toute droite que nous pouvons imaginer partant de notre œil aboutirait nécessairement sur une étoile fixe, nous parviendrait nécessairement ainsi de tout point du ciel ».
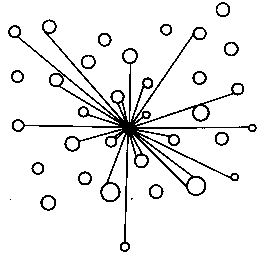
Il émet aussi l’argument que si les étoiles sont à des même distances les unes des autres ou groupés en système semblable à la Voie Lactée, cela n’a que peu d ’effet sur la limite de visibilité.
A l’époque de Chéseaux (
![]() 1744), puis même d’Olbers (
1744), puis même d’Olbers (
![]() 1823), les astronomes sont incapables de réaliser que les
conditions physiques dans un univers à ciel brillant serait tout à fait
semblables à celles régnant dans un four à haute température. Il n’ont pas de
notion de thermodynamique, ils ne pensent pas à la conservation de l’énergie,
ni même ne considèrent la chaleur et la lumière comme des formes convertibles
d’énergies.
1823), les astronomes sont incapables de réaliser que les
conditions physiques dans un univers à ciel brillant serait tout à fait
semblables à celles régnant dans un four à haute température. Il n’ont pas de
notion de thermodynamique, ils ne pensent pas à la conservation de l’énergie,
ni même ne considèrent la chaleur et la lumière comme des formes convertibles
d’énergies.
En 1848, dans sa critique du livre d’ Alexander von Humbold « Kosmos », parue dans «The Edinburgh Review », John Herschell montre que l’explication de la nuit noire de Chéseaux et d’Olbers ne tient guère debout. En effet, dans un univers en équilibre, tout ce rayonnement, partout, doit chauffer les poussières et les nuages obscurs et, si l’équilibre est atteint, les nuages « obscurs » atteindront la même température que celle du rayonnement qui baigne l’univers.
Et le paradoxe persiste !
Il évoque dans ce même livre la possibilité d’une structure hiérarchique comme solution à l’énigme de l’obscurité. Même si les étoiles sont en nombre infini, dit-il, le ciel ne luit pas nécessairement d’une lumière stellaire en tout point, comme l’a envisagé le docteur Olbers.
« Rien n’est plus facile que d’imaginer dans l’espace des arrangements systématiques d’étoiles (…) en accord avec ce que nous voyons autour de nous. »
Remarque sur la limite de visibilité
En admettant une étoile du type solaire pour un volume de dix parsecs cube (un parsecs équivaut à 3.26 années lumière), on trouve que λe=1014 années lumière environ.
Si au lieu de considérer les étoiles comme les éléments qui constituent l’univers homogène sur lequel nous fondons nos calculs, nous considérons les galaxies, nous en prendrons 0.02 par mégaparsecs cube, et nous donnerons à chacune un rayon de 10 000 parsecs ; le calcul aboutit alors à une valeur de l’ordre de λg=1019 années lumière.
On trouve donc des valeurs de λ nettement plus grandes que les dimensions de l’univers exploré jusqu’à aujourd’hui (Ro=1010 années lumière). Autrement dit, l’horizon ne joue guère de rôle dans notre ciel et n’élimine pas le paradoxe : les étoiles ou les galaxies ont des dimensions apparentes trop fines pour se cacher l’un l’autre dans les limites de notre champ d’observation.
L’éclairement produit par un ciel rempli uniformément d’étoiles est indiqué ici en fonction du rayon de l’univers vu par l’observateur. Dans le cas d’étoiles ponctuelles, l’éclairement est proportionnel au rayon de l’univers « vu » (droite α) et, dans le cas d’étoiles comparable au soleil, en éclat et en dimension, l’éclairement est constant (droite β) et égal à celui du soleil après la limite de visibilité. R0 désigne ainsi l’univers exploré. Les points d’interrogations ne peuvent être levés que par une théorie cosmologique complète.
Le rayon Ro de l’univers exploré est inférieur à λ(λe ou λg) ; on est sur la première partie linéaire de la courbe représentant l’éclairement en fonction u rayon de l’univers. Cet éclairement est nécessairement inférieur à l’éclairement produit par le soleil. Si l’univers était fini et que ses dimensions soient seulement un peu plus élevées que λ ,l’éclairement du récepteur serait celui dû au soleil, multiplié par Ro/λ (voir relation (17) de Kelvin) soit 10-4(pour λe) ou 10-9 (pour λg) . Autrement dit, le ciel aurait un éclat de l’ordre de –19 magnitudes par degré carré (pour λe) ou de –6.5 magnitudes par degré carré (pour λg). Or, l’éclat mesuré, en dehors de l’atmosphère, est beaucoup plus faible, seulement +5 magnitudes par degré carré.
Ceci a une double signification :
- Si l’univers fini explique les observations, il doit être terriblement « lacunaire », (différent de notre univers proche qui servi au calcul de λ ) et ceci que l’on considère un univers d’étoiles ou de galaxies.
- Si l’univers n’est pas fini, sa structure est encore plus nettement lacunaire puisqu’il faut intégrer sur d’immenses distances.
Cette constatation a donné naissance à une description cosmologique lacunaire, d’un intérêt majeur, celle des univers hiérarchisés.