Pour résoudre le « paradoxe d’Olbers », on peut enlever l’hypothèse (a): « les étoiles (ou les galaxies) sont distribuées uniformément » en spéculant l’existence d’un univers structuré (fractal).

Lambert dans « lettres cosmologiques »(1761) et Kant dans son ouvrage « Histoire Naturelle Universelle » (1755) en décrivent le principe sans entrer dans les détails.

« ….

Notre terre appartient à une foule de systèmes dépendants les uns des autres, et qui vont en croissant graduellement  elle est donc comprise dans la sphère d’activité de chacun des corps qui les régissent, et par conséquent dans celle du soleil, dans celle du corps qui régit notre système de fixes, des voies lactées , ainsi de suite  chacun de ces corps régissants devrait occuper un espace remarquable dans le ciel, et pouvoir être distingué au moyen du télescope , si aucun obstacle ne s’y opposait  mais je ne pense pas qu’il fût possible d’en apercevoir plus d’un, parce que d’après l’affaiblissement que doit éprouver leur lumière par la matière qui occupe cet espace qui nous sépare, et par cette clarté dont notre atmosphère n’est jamais privée pendant la nuit, une lumière dis-je qui n’est que réfléchie, et qui a un espace aussi immense à parcourir, doit nécessairement faire une trop faible impression sur nos yeux, malgré les secours que nous pourrions attendre du télescope.

« ….

Et alors, si les étoiles fixes composent un système dont l’étendue est fixée par la sphère d’attraction du corps situé en son centre, ne doit-il pas se rencontrer plus de systèmes solaires (ou si l’on veut, plus de Voies Lactées) qui se seraient produits ailleurs, formés dans le champ illimité de l’espace ?…Il y a des systèmes sans aucun doute, ils se sont formés de la même façon, ont été arrangés, organisés par les mêmes processus, et ils ont conservé leur constitution par un mécanisme semblable à tout ce qui gouverne notre propre système.

Si, encore, on considère ces énormes systèmes d’étoiles comme les membres d’une grande chaîne, celle de la nature dans sa totalité, alors, il y a juste autant de raisons que ci-dessus de penser qu’ils on des relations mutuelles, et des connections, qui commande à toute la nature, constituent un système nouveau, encore plus grand, régi par l’attraction d’un corps incomparablement plus considérable, agissant depuis le centre de gravité de ce système gigantesque…Mais quel est la fin de cet arrangement systématique ? La création elle-même va-t-elle cesser quelque part ? Il est évident qu’afin de penser à ce problème comme lié à la puissance de l’Être infini, cet arrangement systématique ne doit tolérer aucune limite.

…. »

En gros, quelle que soit l’échelle à laquelle on l’observe, l’univers est en quelque sorte, selon ces auteurs, semblable à lui-même. L’arrangement hiérarchique de Kant était évolutionniste et d’extension infinie, mais celui de Lambert était statique et fini.

Fournier d’Albe

Dans son petit livre « Two New Worlds », publié en 1907, Fournier envisage plusieurs solutions pour le « paradoxe d’Olbers » :

• une infinité d’étoiles invisibles alignées derrière les étoiles visibles
• la plupart des étoiles sont des corps normalement non lumineux
• si l’univers est d’âge fini, alors l’univers visible est de dimension finie, et par conséquent contient trop peu d’étoiles pour recouvrir le ciel

Il défend aussi dans ce livre le concept d’univers hiérarchisé.

Système hiérarchique de Fournier d’Albe

Le point de départ de la construction de Fournier d’Albe est un octaèdre régulier centré. Les 6 sommets et le centre de l’octaèdre sont censés représenter les objets célestes, et l’ensemble de ces 7 points constitue un amas galactique d’ordre 1. Pour obtenir 1 amas d’ordre 2, on agrandit l’amas précédent d’un facteur 7.

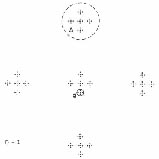
Le cercle a est un amas galactique d’ordre 1, le cercle A un amas d’ordre 2, le toute un amas d’ordre 3,etc.

Dans, un certain volume, supposé sphérique de rayon Ri, la structure hiérarchique H d’ordre i+1 ( H_i+1 ) qui contient 7 systèmes H_i . Supposons que la masse de la structure H_i soit M_i. La structure d’ordre H_i+1 contient 7 fois plus d’éléments, donc M_i+1= 7M_i, or son rayon est

R_i+1=7R_i   alors M_i+1/R_i+1=M_i/R_i=7.    

Donc dans l’univers de Fournier d’Albe : M 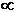R

Justification par Fournier que M est proportionnel à R

Utilisant sans inquiétude une formule qui n’est en principe applicable qu’aux objets à symétrie sphérique, supposons que, sur la surface de tout univers visible (d’ordre arbitraire) de masse M et rayon R, le potentiel gravitationnel Φ est tel que Φ = -GM/R (G étant la constante gravitation ).Une étoile tombant sur cet univers aurait à l’impact une vitesse V tel que :

ΔE_c = -1/2MV²= - ΔE_p = M Φ                        ( Théorème de la conservation de l’énergie)

Donc V=(2GM/R)^1/2

Or, affirme Fournier, l’observation montre que les dites vitesses sont bornées. Si l’on veut que, pour des objets célestes d’ordre élevé, cette vitesse ne tende ni vers l’infini ni vers zéro,  il faut que la masse M croisse comme le rayon R, et non pas (à l’exemple d’une distribution de Poisson) comme le volume (4/3) π R³.

Soit ρ (R) :masse volumique a une distance R de l’observateur

ρ=M/V d'où   ρ 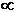  R^-2

Donc un univers hiérarchique construit comme tel possède une intriguante propriété : sa densité moyenne diminue à mesure qu’on la calcul sur des volumes de plus en plus grands, pour tendre finalement vers zéro dans un univers d’extension infinie possédant une infinité de niveaux hiérarchiques.

Carl charlier

Après avoir lu le livre de Fournier d’Albe, Charlier déduisit une solution hiérarchique à l’énigme de l’obscurité nocturne. Il publie en 1908 d’abord, puis en 1922 dans un article plus détaillé intitulé « Comment construire un monde infini ».

Le modèle de Fournier a d’innombrables défauts, dont celui-ci : il est trop régulier. C’est là un aspect que Charlier corrige en laissant N ( : nombre d’étoiles dans la hiérarchie) et r ( : rapport homothétique entre deux hiérarchies) varier d’un niveau hiérarchique à l’autre.

Type du calcul effectué par Charlier  :

D’après (4), la limite de visibilité λ est tel que : λ=V_e/S_e

Avec Ve : volume occupé par une étoile    et Se : section d’une étoile

Considérons un amas sphérique d’étoiles (une galaxie) de diamètre D_G
Or, où que nous nous trouvons dans cet amas d’étoiles, on veut voir au-delà de cet amas, d’où :

Soit V_G : volume de l’amas sphérique, d’où V_G=4/3.π (D_G/2)^1/2=π /6.D_G³ (6)
Soit N_ea : nombre d’étoiles dans l’amas, d’où : V_e=V_G/N_ea (7)

Donc, d’après (5),(6)&(7) :  D_G < [ π /6.D_G³]/[N_ea.π.(D_e/2)²]
(avec D_e : diamètre des étoiles)
D’où : D_G²>  3/2.N_ea.D_e²
Le coefficient n’ayant pas d’importance, vu que les amas d’étoiles (galaxie) ne sont pas trop sphériques, alors : D_G²   >  N_ea.D_e²
D’une façon générale, on trouve D _i²>  N_i.D_i-1²

Donc dans un certain volume, supposé sphérique de rayon R_i, la structure hiérarchique (ou H_i) qui contient N_i systèmes H_i-1 doit être construite tel que  :

    R_i/R_i-1> N_i^1/2   ∀i     (8)    (:résultat de Charlier pour lever le « paradoxe  d’Olbers » ).

Lorsque cette relation est satisfaite à tous les niveaux, cette relation est une condition suffisante pour avoir un univers transparent. Si N=N1N₂N₃…N_i est le nombre total d’étoiles contenues dans le i-ème amas, alors :    N < (R_i/R₀)²      ( où R₀ est le diamètre d’une étoile ).

Une hiérarchie infinie tel que celle de Charlier répond à la condition d’Olbers.

Distribution d’amas dans l’univers

Dès les premières décades du 20^ème siècle, les astronomes ont remarqués « l’amassement » hiérarchique des galaxies. Les résultats d’observations récentes montrent un univers hautement structuré mais également hautement désordonné. Il se révèle en fait moins simple que prévu : à une échelle plus grande que les amas de galaxies, la matière semble organisée en structures aplaties, filamenteuses et lacunaires.

On remarque tout d’abord que les galaxies sont distribuées par paquets à toutes échelles. Notre galaxie c’est-à-dire la Voie Lactée, appartient à ce que l’on appelle le Groupe local d’une vingtaine de galaxies  sa taille est d’environ 1 Mpc (1 pc 3.08.10¹³ km). L’amas le plus proche est ensuite celui de la vierge à environ 10 Mpc de nous, puis la Coma (Chevelure de Bérénice) formée de quelques milliers de galaxies à 100Mpc. Ces amas font eux-mêmes partie de super-amas. Nous appartenons au Super-amas local, découvert par de Vaucouleurs vers 1958. Il a la forme d’un disque d’environ 1Mpc de large sur 10 Mpc de long. Cette hiérarchie locale à laquelle appartient notre galaxie est en fait une structure très générale.

A partir des observations on constate les distributions en masses et distances suivantes :

Les galaxies :

• leur masse représente 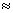10¹² à 10¹⁴ M_o (masses solaires)
• et leur taille 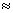10 à 100 Kpc

La moitié des galaxies appartient à des groupes de quelques dizaines avec :

• une masse 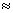 10¹² à 10¹⁴ M_o
• une taille 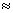1/10 à10 Mpc

Les amas sont formés de quelques milliers de galaxies avec :

• une masse 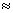10¹⁵ M_o
• une taille 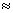10 Mpc

figure relative aux principaux groupes de galaxie
dont la distance à la terre est à 16 mégaprsecs.

Benoit Mandelbrot

En 1974, Mandelbrot, dans « les objets fractals », introduit sa théorie des « nombres fractals », et discute de la distribution des galaxies dans le cadre de cette théorie.

Mandelbrot définit la dimension d’un système parl’exposant D dans la formule reliant la masse M à l’intérieur d’une boule de rayon R (le centre de la boule étant sur la structure fractale :
M(R) 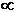   R^D   (9)

(Cette relation est une généralisation de la formule classique reliant, dans un espace de dimension E, le volume V d’une boule à son rayon R (dans un espace de dimension E : V 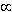R^E))

Pour évaluer le degré d’amassement des galaxies, Mandelbrot se fonde sur l’analyse de la densité  globale de matière contenue dans l’univers développée par l’astrophysicien : Gérard de Vaucouleurs.

Soit M(R) : masse de matière contenue dans une sphère de rayon R ρ(R) : densité de matière contenue dans cette sphère.

Alors ρ(R)=M(R)/[(4/3)πR³]

D’après (8) : ρ(R) 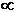R^D-3

Pour obtenir la densité globale de matière dans l’univers, il suffit de faire tendre le rayon R vers l’infini. Malheureusement, la convergence en question laisse fortement à désirer : au fur et à mesure que la profondeur du monde perçu par les télescopes a augmenté, la densité moyenne de la matière n’a cessé de diminuer ( d'où D<3 )

 Or selon les observations de Vaucouleurs, cette densité est resté à mesure que progressaient les observations, proportionnelle à R^D-3, où D est exposant beaucoup plus petit que 3 et même voisin de 1. Les meilleurs estimations lui attribuent le valeur 1.23.

La hiérarchie de l’univers physique selon Vaucouleurs relie le logarithme de la densité d’une structure au logarithme du rayon de la sphère contenant cette structure. On notera le bon alignement (décrite par la relation de Vaucouleurs) des points fournis par les objets réels observés dans le ciel  planètes, étoiles de toutes sortes, galaxies et familles de galaxies. Le dénombrement de Lick marque à peu près les bornes de l’univers bien exploré (R₀). On a figuré aussi la densité du milieu ambiant (zone hachurée) dans lequel baignent les condensation de matière que sont les astres et on note que le contraste diminue quand on va vers des objets de plus en plus grands.

Donc d’après les observations : ρ 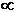R ^D-3 , d’où : M(R) 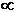R^D

Mandelbrot voit dans cette relation une première indication que D est peut une dimension fractale et donc que l’univers est fractale.

Le fait que cette dimension soit inférieur à la dimension de l’espace ambiant lui-même (trois) reflète l’« intense amassement » des objets célestes constaté empiriquement.

Toute la question est en fait de savoir si D reste constant. Sans prendre position sur le fond, Mandelbrot admet que dans une zone moyenne au moins (correspondant à la zone observée) la dimension fractale de l’univers D reste inférieur à 3. Ces analyses empirico-phénoménologiques permettent de préciser les contraintes théoriques auxquelles doit satisfaire un modèle fractal acceptable de l’univers. Celles-ci sont doubles :

1) il faut d’abord que ce modèle reflète la structure hiérarchique des objets célestes (l’amassement)

2) il faut ensuite qu’il ait une densité globale de matière nulle, ou plus précisément que M(R) soit proportionnel à R^D, D étant un exposant fractionnaire inférieur à 3 dont la valeur doit être fixée empiriquement.

Remarque sur la dimension de l’univers Fournier d’Albe

Dans l’univers de Fournier, chaque amas d‘ordre (i+1) est l’image homothétique (dans le rapport S=7) de l’amas d’ordre i et contient N=7 amas d’ordre i.

Mandelbrot définit la dimension homothétique tel que : N=S^D      (10)

N : nombre d’éléments
S : rapport homothétique
D : dimension homothétique

Donc la dimension homothétique (fractale) de l’univers de Fournier est D=ln7/ln7=1 .

Sa dimension topologique est nulle, puisqu’il est constitué par une infinité de points.

Une structure fractale possède toujours une dimension fractale supérieure à sa dimension topologique (la dimension topologique correspond en général à la dimension analytique traditionelle)

D’après la relation (8), le ciel reste sombre si N_i<(R_i/R_i-1)² .
La masse M_i de la hiérarchie H_i est tel que : M_i=N_i.M_i-1 . (12)
Donc d’après (8) & (12) : M_i/R_i² < M_i-1/R_i-1²
Or d’après (9), M(R) 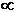R^D
Alors R_i^{(D 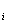-2)}< R_i-1^{(D -2)} ,  or R_i > R_i-1>0
Donc, il faut que D_i-2 <D_i-1-2<0
Donc la condition : D _i <2  ∀i ( ou D _max < 2 )     évite le « paradoxe d’Olbers ».