En 1676, Römer remarque, comme Cassini quelques années plus tôt, des irrégularités dans les éclipses du satellite Io de Jupiter par rapport aux prévisions. Il explique que les immersions du satellite derrière Jupiter et ses émersions se produisent rarement à l’heure prévue à cause du fait que la lumière a une vitesse finie .

Or une vitesse finie signifie qu’à l’instant de son observation, un objet n’est pas ce qu’il paraît être.  Il s’est non seulement déplacé, mais il a également changé d’apparence. Les conséquences de ce concept révolutionnaire (que l’âge de l’univers ne peut-être inférieur à l’étendue de l’univers visible divisée par la vitesse de la lumière) mirent longtemps à pénétrer les mentalités de l’époque.

Edgar Allan Poe

En 1848, le poète et scientifique amateur Edgar Allan Poe publie un essai intitulé : « Eureka : A Prose Poem » (Voir Annexe 3). Eureka fut d’abord lu cette même année en conférences publiques sous une forme qui nous est inconnu. Il essaye en particulier de résoudre le « paradoxe d’Olbers ». Sa solution est que la lumière émise des étoiles ne nous est pas encore parvenu. La vitesse de la lumière et l’âge des étoiles se rencontraient enfin pour révéler un aspect nouveau d’un problème ancien .

William Thomson (Lord Kelvin)

En 1884, lors d’une conférence à Baltimore (publié en 1901 et 1904), Kelvin fait allusion au « paradoxe d’Olbers ».

Son calcul

Hypothèse : toutes les étoiles :

• sont semblables au soleil
• sont distribuées uniformément
• ont un rayon a

Soit ρ : densité d’étoiles dans l’espace

D’après (1), la fraction du ciel recouverte d’étoiles dans une couche sphérique de rayon r et d’épaisseur dr est : πa²ρdr .

Pour tenir compte du recouvrement géométrique (c’est-à-dire de l’occultation due aux étoiles contenues dans les couches intermédiaires (négligé par Kelvin)), il faut multiplier ce nombre par exp(-r/λ) , où λ= 1/(ρπa²)  (d’après (2)) est la limite de visibilité.

La fraction du ciel recouverte par les étoiles de cette couche est donc  :λ^-1.exp(-r/λ)dr  

D'où α = 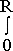λ^-1.exp(-r/λ)dr = 1 - exp(-R/λ)          (13)

avec α : fraction du ciel recouverte par les étoiles jusqu’à un rayon R.

Si la répartition stellaire est d’extension infinie, le ciel est entièrement recouvert (α=1) et la distance de visibilité depuis un point quelconque est égale à la limite de visibilité λ.

On obtient le résultat de Kelvin lorsque le rayon r est petit devant la limite de visibilité : α 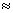R / λ = Rπρa²   :
α 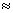(Dimension de l'Univers visible)/(Limite de visibilité)         (14)

Soit N : le nombre total d’étoiles, alors N=4/3πR³ρ

Donc α=3/4N.(a/R)²          (15)

Ce traitement de Kelvin clarifie ceux donnée par Halley en 1721, Chéseaux en 1744, et Olbers en 1823.

Supposons que chaque étoile ait une luminosité égale à L. La contribution à la densité de rayonnement u au centre de la couche sphérique vaut du = (ρL/c).exp(-r/λ)dr

Et donc   u = 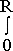du = u ^* . (1-exp(-R/λ))

Avec u^* =L/(πa²c) : densité de rayonnement à la surface d’une étoile.

On voit ainsi que u = u^* pour toute distribution stellaire s’étendant au-delà de la limite de visibilité.

Des équations (13) et (15), on tire : α= u/u^*     (16)

Ce qui démontre la vérité de l’énoncé de Kelvin selon lequel «  a est le rapport de la luminosité apparente de notre ciel étoilé à la luminosité du disque de notre soleil ».

Donc d’après (14)&(16), on a : α = R/λ =u/u^*    (17)

Cela signifie que si la dimension de l’univers visible était égale à la limite de visibilité, le ciel nocturne était en tout point aussi brillant que le disque solaire. La luminosité globale du ciel nocturne doit donc donner un aperçu de la taille de l’univers visible, soit qu’il fût de taille réellement finie, soit que la lumière n’avait pas encore eu le temps de nous parvenir des régions éloignées.

calculs numériques de Kelvin

Il prit l’hypothèse que les étoiles sont uniformément réparties dans une sphère de rayon égal à R=3,09.10⁹ km, que N=10⁹ et que a=7.10⁵ km. d'où R/a = 4,4.10¹⁰

Or selon (15), α = 3/4N(a/R)² , alors α = 3,87.10^-13<<1

Or si on veut que α 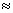4% = 4.10^-2 (≡ rapport de la luminosité apparente de notre ciel étoilé à la luminosité du disque de notre soleil ),

Alors il faut prendre un rayon de 10¹¹.R, soit 3,09.10²⁷ km.

Or c=300 000 km .s^-1, alors la lumière des soleil périphérique de notre grande sphère métrait 3,27.10¹⁴ années à nous parvenir.

Les calculs de Kelvin, basés sur les données astronomiques de l'époque, montrent que la limite de visibilité est à une distance de 3 000 billions d'années-lumière. (Son résultat n’est en fait qu'un dixième de cette valeur, car il ne considère qu'un ciel partiellement recouvert.) La limite de visibilité est donc un billion de fois plus grande que la Galaxie. En supposant qu'aucune étoile n'existe à l'extérieur de la Galaxie, les disques stellaires ne peuvent recouvrir qu'un billionième du ciel, et chaque point du ciel doit être un billion de fois moins brillant que le Soleil.

Mais, même si nous occupions un Univers empli d'étoiles, une « grande sphère » d'étoiles d'un rayon de 3 000 billions d'années lumière, dit Kelvin, le ciel nocturne ne serait pas encore recouvert d'étoiles parce que l'Univers visible aurait un rayon très inférieur a 3 000 billions d'années-lumière. La lumière doit mettre 3 000 billions d'années « pour voyager des étoiles périphériques de notre grande sphère jusqu'à son centre » où nous nous trouvons.

Kelvin s'est intéressé toute sa vie au problème de la détermination de l'âge de la Terre et du Soleil. Au début, il suppose que le Soleil puisait son énergie lumineuse dans la chaleur produite par la chute de météores. Puis dans un essai intitulé « Sur l'âge de la chaleur du Soleil » (1862), il écrit : « Ainsi, soit le Soleil a été créé comme source active de chaleur, par un décret supra-souverain, à une époque qui n'appartient pas à des temps immémoriaux , soit la chaleur qu'il a déjà rayonnée, et celle qu'il possède encore, lui ont été fournies par un processus naturel obéissant à des lois définitivement établies. Reprenant une idée initialement avancée par Julius von Mayer et défendue par Hermann von Helmoltz , il suppose que le Soleil tire son énergie lumineuse de sa lente contraction gravitationnelle. Et donc, en admettant que le soleil ne pouvait initialement être plus gros que l’orbite de Mercure, et en supposant une contraction assez importante pour maintenir le soleil à sa luminosité actuelle (de quelques dizaines de mètres par an), il obtient pour l’âge du soleil une valeur d’environ 30 millions d’années (100 millions d’années au maximum).

« Ainsi, dit Kelvin, si toutes les étoiles de notre immense sphère ont commencé de briller en même temps ( ... ) la lumière atteignant la Terre à chaque instant ne proviendrait au plus que d'une quantité d'étoiles extrêmement limitée». Lord Kelvin démontre rigoureusement ce qu'Edgar Allan Poe avait qualitativement prévu: que la limite de visibilité est « si considérable qu'aucun rayon lumineux n'a pu encore nous en parvenir ».